On Synth Terminology: Frequency (Everybody Hertz, Sometimes)

An original Minimoog and ARP 2600 from the studio of Amin Bhatia.

Both hardware and software synthesizers are highly technical electronic musical instruments, though thankfully you don't need to be an electrical engineer or a computer programmer to operate them. Still, many of their controls are labeled with technical terms that we would do well to understand to get the most out of our synths.

One of these terms, frequency, is often used to label several seemingly unrelated controls, thus causing confusion as to what function they serve. So let's find out what frequency is all about and how it relates to synthesizers, audio, and music in general.

Frequency!

In the fields of audio and music, the term frequency refers to how often — how frequently — something repeats or cycles within a one-second period of time.

Certainly, repeating and cycling are what audio oscillators do when they generate audio waves, and how rapidly this occurs has a direct bearing on the pitch we hear. For example, an oscillator has to generate a repeating waveform 27½ times per second to produce the same pitch as the lowest note on a piano, low A. Now, 27.5 cycles per second, or 27.5 Hertz (27.5 Hz) may seem like a pretty fast rate of speed considering that you couldn't possibly clap your hands that quickly! But by comparison, an oscillator has to repeat its pattern more than 4,100 cycles a second to match the note produced by the highest C on a piano (4100 Hz, or 4.1 KHz).

Thus, and to generalize, we can refer to low pitches as “low frequencies” and high notes as “high frequencies”. And while it may seem a bit dispassionate to refer to musical tones as mere frequencies, we can see the correlation in using the term frequency to label certain controls used to adjust an oscillator's pitch. (See Figures 1 and 2).

FIGURE 1: The Minimoog's frequency controls for oscillators 2 and 3 (large knobs) and their octave switches (which also control their frequency).

FIGURE 2: The nondescript oscillator frequency controls for the ARP.

Elephant Talk

Many synths feature one or more oscillators specifically designed to generate repeating waveforms in the sub-audio range. This is a range of frequencies that elephants and whales are known to communicate with, though they're far below that what humans can hear due to the low frequency of the oscillations. Here I'm talking about LFO's — low frequency oscillators — typically used as “repetitive pattern generators” for creating cyclic undulations in pitch (vibrato), filter (wobble), and amplitude (tremolo).

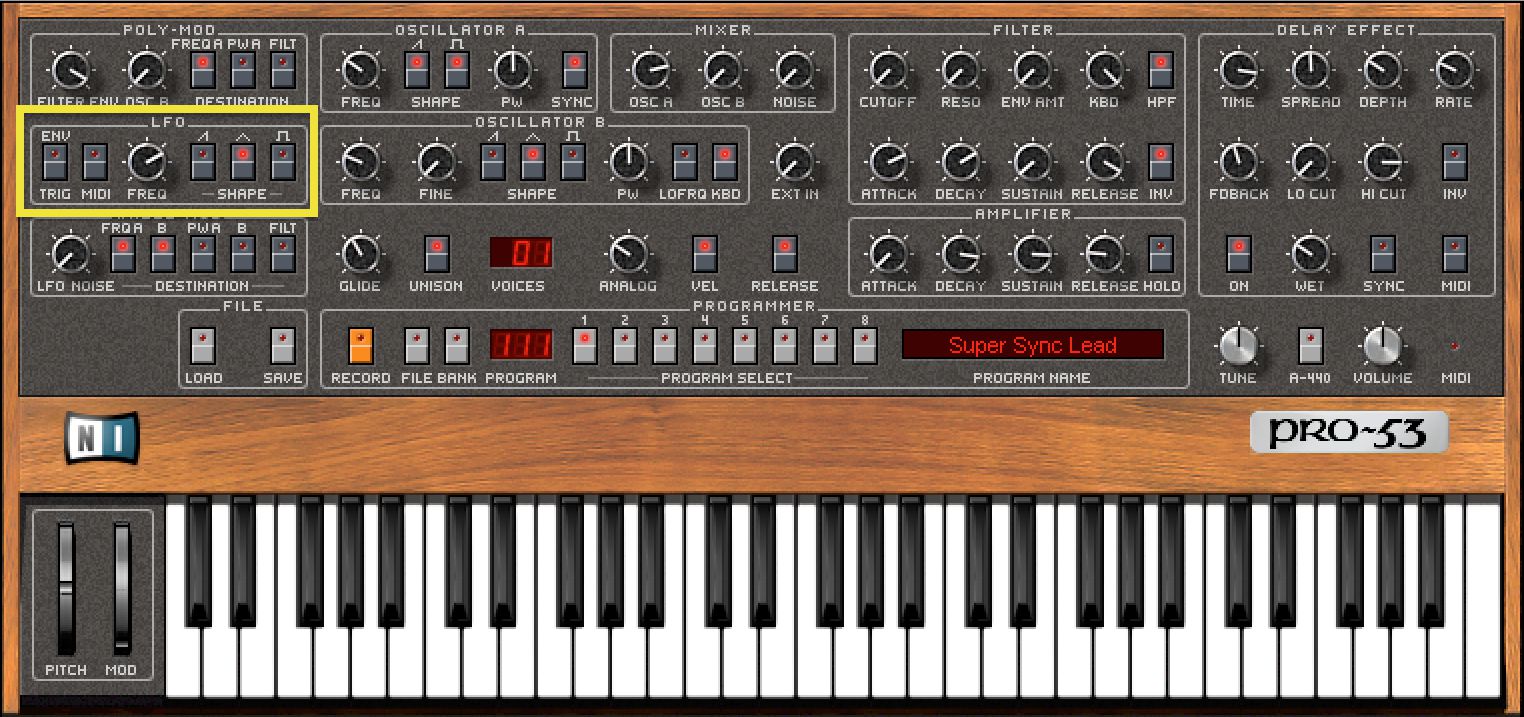
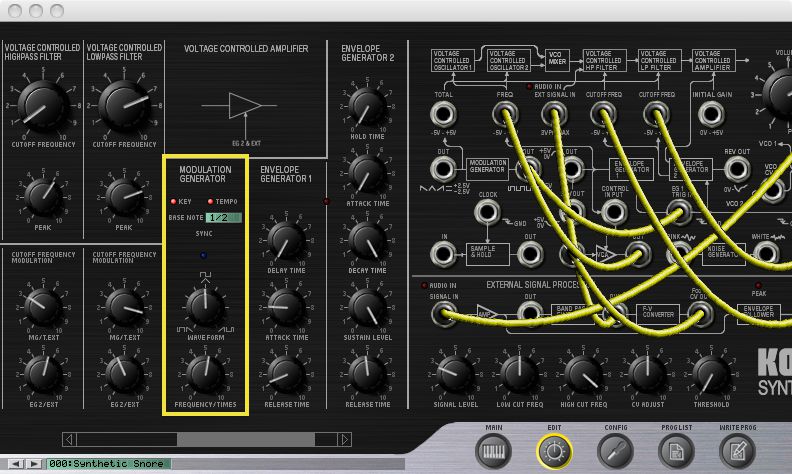
And when it comes to setting the rate of speed at which these oscillators repeat their patterns, it's common to see their controls labeled rate, speed, or once again, frequency. (See Figure 3 and 4).

FIGURE 3: LFO controls on the Pro-53.

FIGURE 4: The Korg MS-20's Modulation Generator (their term for LFO).

As a side note, because LFO's generate sub-audio range signals, you'll rarely find them connected to the audio path in most synthesizers. After all, if only elephants and whales could hear them, why bother?

Filters and Frequency

So far, we've seen examples of how the term frequency pertains to various kinds of oscillators. Now let's examine why this same term is used to label one of the primary controls used in shaping the tonal quality of a sound: the cutoff frequency control of a lowpass filter — the type of filter built into just about every synth ever made. 

FIGURE 5: Filter Frequency control on the ARP 2600.

First, Some Fundamentals

When an audio oscillator generates sound, the pitch we perceive is directly attributable to the frequency at which it produces its repeating waveform pattern. However, it's only when an oscillator is set to generate sine waves that we'll hear just that frequency alone, and here's why…

FIGURE 6: A sine waveform (two cycles).

Sine waves are the simplest possible audio waveform shape, producing a “pure tone”. Anything simpler, or more pure, would be silence! 

On the other hand, complex waveshapes such as sawtooth, square, pulse, and triangle waves get their distinctive timbre because some number of harmonics or overtones are “embedded” in the sound. In short, think of harmonics as an additional layer of frequencies (notes) pitched higher than the fundamental note itself, but so low in volume that they serve to color the sound without being heard as distinct pitches.

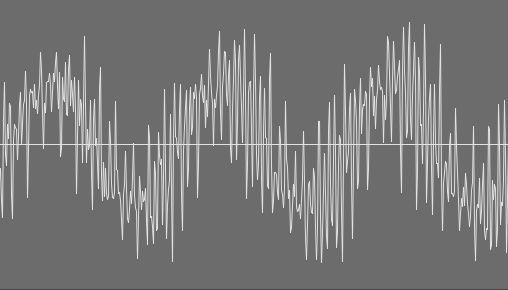
FIGURE 7: A very complex waveshape made on the ES-2 synth plugin (Logic).

FIGURE 8: Sawtooth waveform (two cycles), also a “complex” wave.

For example, let's take a sawtooth wave being generated by an audio oscillator at a frequency of 250 Hz, approximately middle C (C3). That frequency is the note's fundamental pitch, the very frequency we identify as the note C3.

But in addition to the fundamental at 250 Hz, the sawtooth sound also contains many higher-frequency harmonics. The first one is pitched an octave higher than the fundamental at 500 Hz (2x the fundamental's frequency). The next harmonic occurs at 750 Hz (3x the fundamental's frequency), with more harmonics at 4x, 5x, 6x, 7x, and so on. In fact, the harmonics produced by a real analog synth's sawtooth wave can number in the dozens, with their frequencies extending far into the upper ranges of human hearing (20 KHz) and beyond (see Figure 9).



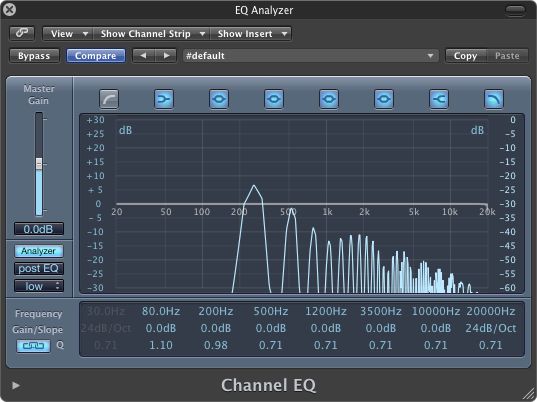
Figure 9: Frequency Analyzer showing the relative volume level of the fundamental (the first bump) and harmonics (all of the other bumps) contained in a 250 Hz sawtooth wave.

Tuning it In to Tune it Out

It's the presence of these harmonics that give sawtooth waves their bright, buzzy tone, though we can make this sound duller by using a lowpass filter to cut off some of those higher “buzzing” frequencies. Indeed, when you lower the cutoff frequency control on a lowpass filter, what you're actually doing is tuning it in to target harmonics starting at a particular frequency. Any frequencies higher than that setting will be significantly reduced in volume (cut off), thus dulling the sound. And that's why it makes perfect sense for the filter's cutoff control to be labeled… frequency! 

FIGURE 10: Filter Frequency control on the Minimoog.

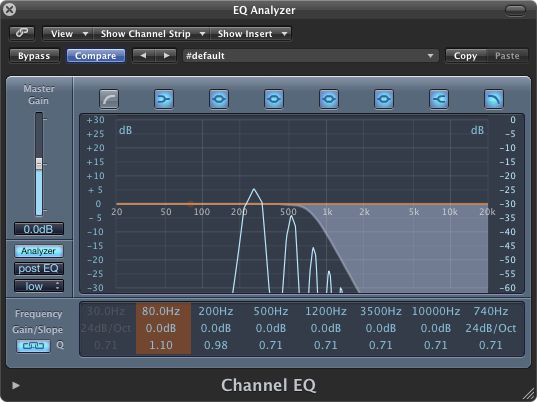
FIGURE 11: Filtering the 250 Hz sawtooth wave at a cutoff frequency of 740 Hz. Compare the strength of the harmonics to that in Figure 9 above.

Sine-onara?

Now you know why, when an oscillator is set to output a sine wave, the filter's cutoff control will have little effect on the sound; the absence of harmonics means that there's no harmonic “meat on the bone” for the filter to act upon. But of course, with brighter waveforms, the filter can have a profound effect on the tone.

However, it is entirely possible to tune a lowpass filter's cutoff frequency so low as to actually cut off the fundamental frequency of any waveform! For example, if the cutoff frequency of your filter is set to 80 Hz, but the note you're feeding it is our pitch at 250 Hz, you won't hear much of anything at all come out the other end! (See Figure 12). So when it comes to cutting off frequencies with a lowpass filter, any and all frequencies are fair game.

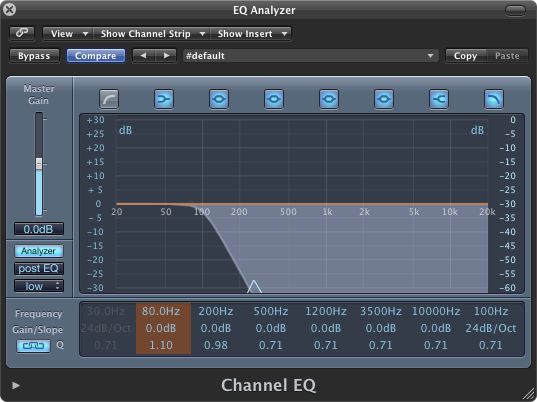
FIGURE 12: Filtering the 250 Hz sawtooth wave at a cutoff frequency of 100 Hz.

Many Thanks!

In closing, photo ops and props go out to Amin Bhatia, my dear friend and composer whose ground-breaking work, Interstellar Suite, re-released this year on its 25th anniversary, was performed on some of the very synthesizers illustrated above.